17/10/2011
La prédation - Relations mangeur-mangé
 La prédation - Relations mangeur-mangé
La prédation - Relations mangeur-mangé
par André Guyard
(mise à jour du 24/05/2012)
On réserve le terme de prédateurs aux seuls mangeurs d'animaux vivants. Cependant, il existe une dynamique commune au phénomène mangeur-mangé qui justifie une approche du phénomène prédation au sens large. En ce sens, sont considérés comme prédateurs la totalité des animaux non détritivores : herbivores, carnivores et parasites et les conclusions qui suivent peuvent leur être appliquées.
I. Modèles mathématiques de la relation proie-prédateur
Les premières tentatives de modélisation mathématique de la dynamique du système proie-prédateur sont dues aux biomathématiciens Lotka (1925) et Volterra (1926). Ils supposent au départ une croissance exponentielle des populations naturelles. Soit N l'effectif de la population de proies et soit P l'effectif de la population de prédateurs.
1. Population de proies
En l'absence de prédateurs, on a :
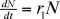
En présence de prédateurs, on aura :
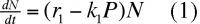
k1 : coefficient qui mesure l'habileté du prédateur à capturer sa proie.
2. Population de prédateurs
En l'absence de proies, la population de prédateurs décroît de façon géométrique :
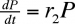
En présence de proies, on aura :
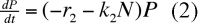
k2 : coefficient qui mesure l'efficacité de la prédation sur les effectifs de la proie.
Le système est en équilibre quand
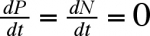
soit quand (r1 - k1 P) = 0 et (-r2 + k2 N) = 0
ou P = r1 / k1 et N = r2 / k2
Des équations (1) et (2), on déduit :
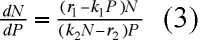
soit, en effectuant le produit des extrêmes par les moyens et en divisant par NP
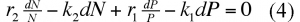
En intégrant l'expression (4) on trouve
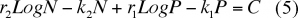
où C est une constante d'intégration.
La représentation graphique de l'expression (5) est une famille de courbes fermées et "concentriques", une courbe particulière correspondant à chaque valeur de la constante (fig. 1).
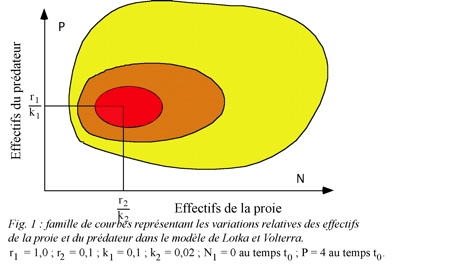
À chaque courbe correspond un "centre" ou point d'équilibre dont les coordonnées sont :
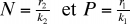
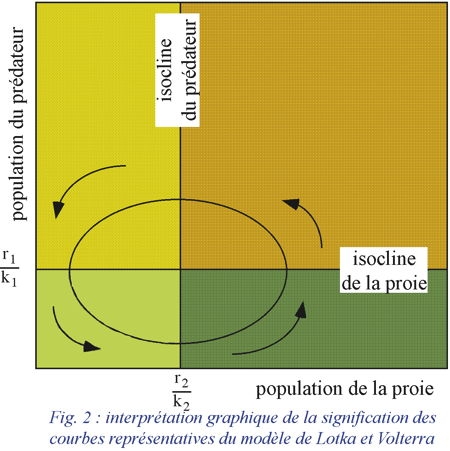
Si l'on se rapporte aux courbes représentatives de (5), on constate que les valeurs N et P vont augmenter puis diminuer de façon cyclique. La figure 2 permet de distinguer plusieurs domaines dans le diagramme qui figure les fluctuations de l'effectif des prédateurs en fonction de ceux de la proie. On distingue 4 régions dans ce diagramme délimité par deux droites, l'une verticale (isocline du prédateur) l'autre horizontale (isocline de la proie [1]). Au-dessous de l'isocline de la proie, la population de celle-ci augmente à cause du nombre limité de prédateurs ; au-dessus elle décroît à cause de la forte pression de prédation. La population de prédateurs augmente à droite de l'isocline du prédateur à cause de la forte population de proies, mais décroît à gauche de cette ligne à cause de la raréfaction de celles-ci. Le déplacement de l'équilibre s'effectue dans le sens inverse des aiguilles d'une montre. Le modèle permet de prévoir que les deux populations du système vont fluctuer de façon cyclique entre un minimum et un maximum, les oscillations présentant un déphasage puisque le début des périodes de croissance et de décroissance des effectifs du prédateur s'effectue en retard sur les périodes correspondantes pour la proie.
Il est d'ailleurs possible à partir des expressions (1) et (2) de calculer les fluctuations des effectifs de la proie et du prédateur en fonction du temps. On obtient par intégration :
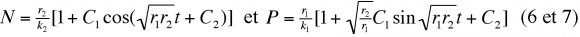
où C1 et C2 sont des constantes d'intégration.
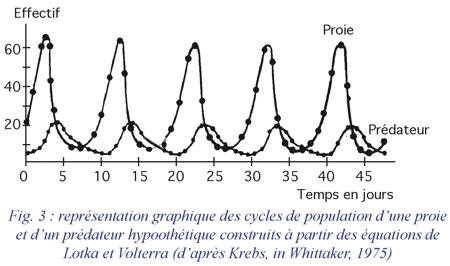
La figure 3 donne l'exemple d'une représentation graphique des cycles des populations d'une proie et d'un prédateur hypothétiques, construits à partir des équations précédentes.
On peut déduire des équations de Lotka et Volterra un ensemble de lois.
II. Lois de la prédation
1. Loi du cycle périodique
Les fluctuations des deux espèces dans le temps sont périodiques et de période
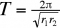
Cette période ne dépend donc que des taux intrinsèques d'accroissement des populations considérées. Les oscillations des populations du prédateur et de la proie sont décalées d'un quart de cycle (figure 3).
2. Loi de la conservation des moyennes
La moyenne du nombre d'individus de chaque espèce ne change pas, quelle que soit la valeur initiale des effectifs, tant que les coefficients r1, r2, k1 et k2 restent constants.
3. Loi de la perturbation des moyennes
Si l'on élimine une égale proportion des deux espèces, on atteint un nouvel état d'équilibre avec augmentation de la moyenne du nombre d'individus de la population de la proie et une diminution de celle des prédateurs [2].
III. Critique et extension du modèle
Le modèle de Lotka et Volterra est fondé sur un certain nombre d'hypothèses simplificatrices très éloignées de la réalité. En effet :
- il n'intègre pas la capacité limite du milieu pour la proie dont la croissance n'est pas supposée dépendre de la quantité de nourriture disponible ;
- il suppose aussi que le prédateur est strictement monophage et ne dispose pas de proies de substitution, ce qui est rarement le cas dans les communautés naturelles ;
- il admet que le taux de prédation est constant, indépendant de la densité et néglige la structure d'âge de la population ;
- il ignore l'existence de temps de latence qui tendent à rendre instables les interactions proie-prédateur. En effet, ces temps de latence peuvent amplifier les oscillations et même conduire à l'extinction d'une des deux populations.
La capacité limite peut être prise en compte dans les équations de Lotka et Volterra.
Soit K1 celle de la proie et K2 = bN, où b est une constante, celle du prédateur, on pourra écrire :
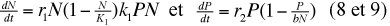
On démontre également que ce système d'équations décrit une interaction stable. Il est également nécessaire de tenir compte du fait que les prédateurs ne vont pas consommer leurs proies proportionnellement à leur abondance. Il faut donc intégrer l'ensemble réponse fonctionnelle-réponse numérique dans le modèle (voir plus loin). Il sera alors nécessaire d'introduire un facteur de saturation C auquel Holling attribue la valeur suivante :
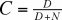
où D est une constante.
Dans ces conditions, les équations deviennent :
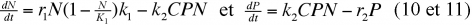
On démontre que de telles expressions permettent d'atteindre des points d'équilibre (attracteurs étranges de Mandelbrot) mais aussi peuvent présenter des fluctuations cycliques. Les cycles obtenus ont des limites stables, c'est-à-dire qu'ils présentent une amplitude et une valeur moyenne des effectifs dans un environnement constant et peuvent retourner à cet état initial après une perturbation.
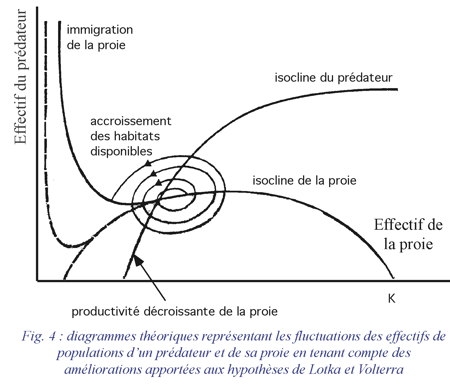
Enfin, un équilibre stable peut être obtenu en tenant compte de la possibilité que peut avoir une proie d'échapper au prédateur en se dissimulant dans un refuge. D'autres modèles mathématiques que nous ne développerons pas ici intègrent également cette donnée ainsi que l'existence de temps de latence. La figure 4 représente un diagramme figurant un tel modèle. On constate que l'élévation de l'isocline de la proie aux faibles densités peut stabiliser une amplification de la trajectoire en spirale de la population provoquée par un temps de latence dans la réponse du prédateur.
IV. Réponse des prédateurs aux variations de densité de la proie
Holling (1959, 1965) distingue une réponse fonctionnelle et une réponse numérique.
1. Réponse fonctionnelle (DN : variation du nombre des proies consommées)
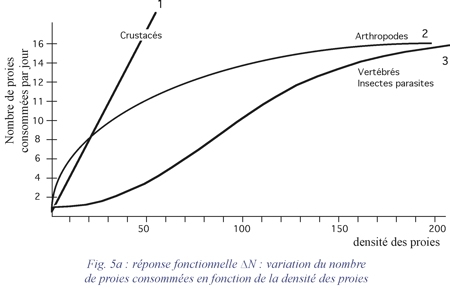
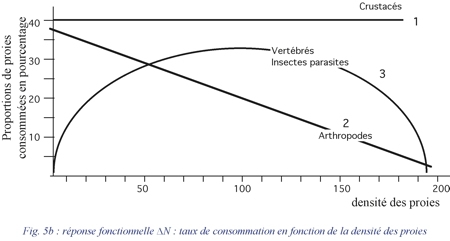
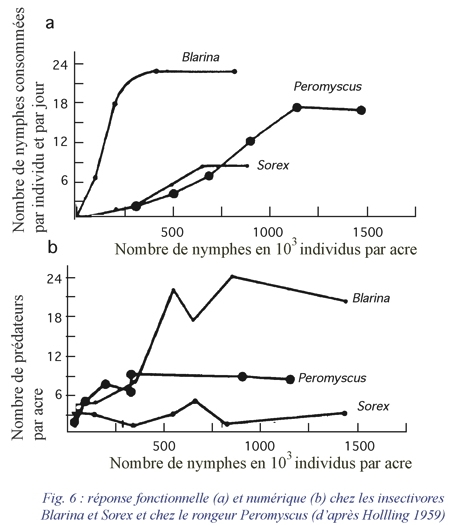
La réponse fonctionnelle d'un prédateur aux variations de densité de la proie se mesure par les variations du nombre moyen de proies DN consommées par individu et par jour. Holling distingue trois types de réponses fonctionnelles (fig. 5a, 5b et 6a):
- La réponse de type 1 est une fonction linéaire de la densité des proies jusqu'à une valeur limite au-delà de laquelle le nombre de proies consommées par individu reste constant quelle que soit la densité (Crustacés) ;
- La réponse de type 2 est caractérisée par un taux de consommation décroissant de façon régulière en fonction de la densité des proies (Arthropodes) ;
- La réponse de type 3 est caractérisée par une courbe en S en fonction de la densité des proies (Vertébrés, Insectes parasites).
La réponse fonctionnelle d'un prédateur à la densité de sa proie principale dépend aussi de l'abondance des proies secondaires. Il y a toujours tendance pour le prédateur à diversifier son régime alimentaire. On peut noter parfois une variation du taux de préférence (effet de bascule ou switching) vis-à-vis de deux sortes de proies.
2. La réponse numérique (DP : variation du nombre de prédateurs)
se mesure par la densité de la population du prédateur et exprime les variations de celle-ci en fonction de la densité des proies (fig. 6b).
Le prédateur ne peut répondre à une augmentation de la densité de sa proie qu'en augmentant son propre taux de croissance et/ou par l'immigration. De sorte que la réponse numérique est la résultante de plusieurs phénomènes différents:
- variations du taux individuel de croissance ou de la durée de développement ;
- variations du taux de fécondité (taille des pontes ou fréquence de reproduction) ;
- variations du taux de mortalité ;
- déplacement de populations provoqués par l'abondance ou la pénurie de proies.
Parmi les phénomènes de déplacements, on distinguera :
- les migrations sensu stricto à déterminisme saisonnier ;
- les émigrations notamment de jeunes consécutives à une pénurie trophique effective (dispersions de saturation) ;
- les nomadismes adaptatifs qui précèdent la pénurie (dispersions de pré saturation). Ex : migrations exploratoires de rapaces précédant la raréfaction des rongeurs (fluctuations synchrones de la densité des proies et des prédateurs). On rejoint ici la réponse agrégative (Hassell, 1986) à la répartition par taches de proies, composante de la réponse fonctionnelle qui a des effets sur la réponse numérique.
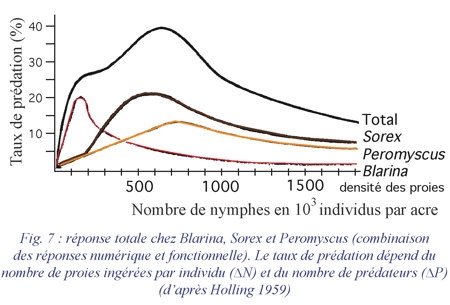
3. La réponse totale
correspond à la combinaison des réponses numérique et fonctionnelle (fig. 7). Il est évident que le taux de prédation dépend de la quantité de proies ingérées par individu et du nombre de prédateurs.
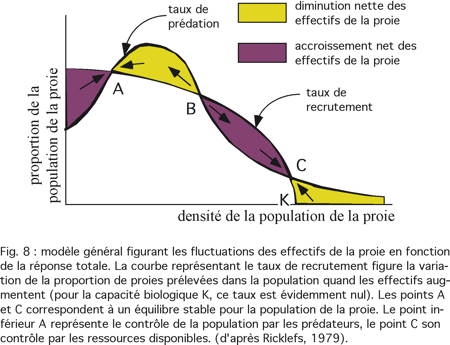
Il est possible d'établir un modèle général qui figure les fluctuations de la population de la proie en fonction de la réponse totale (fig. 8).
V. Conclusion
L'existence de fluctuations cycliques des effectifs des populations de prédateurs et de leurs proies suggèrent que prédateurs ou parasites exercent une action déterminante sur les populations des espèces dont ils dépendent.
Expérimentalement, Gause (1934) a étudié la prédation de Paramecium caudatum en culture par un autre protozoaire cilié, Didinium nasutum (fig. 9).
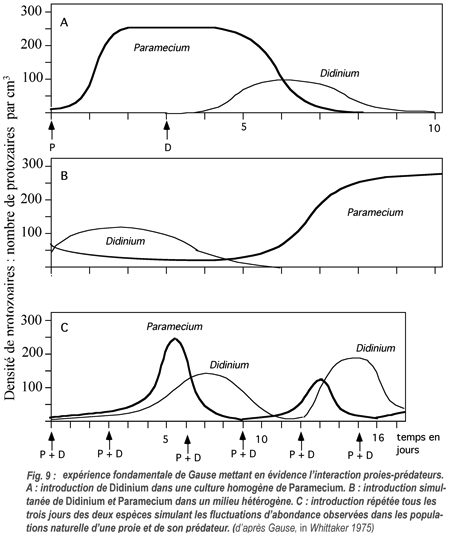
Dans une première expérience, l'introduction de Didinium dans une culture de Paramecium âgée de 3 jours se traduit par la consommation de toutes les proies, de sorte qu'après l'éradication des Paramecium, la population de Didinium périt d'inanition.
Dans une deuxième expérience, les Paramécies et les Didinium sont introduits simultanément dans la culture, des sédiments ayant été placés dans le fond des récipients, offrant un abri aux proies. Après une phase initiale de croissance, la population de Didinium ayant consommé toutes les paramécies accessibles, périclite et périt d'inanition. Les paramécies survivantes vont pouvoir alors proliférer.
Dans une troisième expérience, Gause simule les fluctuations d'abondance proie-prédateur observées dans les populations naturelles par l'introduction simultanée dans la culture de la proie et de son prédateur tous les trois jours, Il obtient alors des oscillations périodiques entretenues des effectifs des populations des deux espèces.
D'autres expériences montrent que, dans un environnement constitué par une mosaïque complexe d'habitats, la relation prédateur-proie s'accompagne d'une certaine stabilité des populations.
Dans la nature, Errington (1963) soutient que les prédateurs ne font que prélever le surplus de la population de toute façon condamné : individus privés d'abris, de territoires, jeunes, déficients ou malades.
D'après Slobodkin (1968), la stratégie optimale des prédateurs serait de consommer ce surplus plus accessible (intérêt), épargnant ainsi le capital population.
Krebs (1978) expose cette stratégie optimale qu'on peut résumer ainsi :
- les prédateurs choisissent les proies les plus profitables qui présentent le meilleur rapport énergie récoltée/énergie de capture et d'ingestion ;
- les prédateurs tendent à concentrer leur effort de chasse là où les proies sont les plus abondantes (réponse d'agrégation du prédateur).
Pour une certaine gamme de densité des proies, le taux de prédation tend à augmenter avec la densité des proies. Ce qui aboutit à une régulation des populations de proies (régulation densité-dépendante), ce mode de régulation n'étant qu'une composante des mécanismes qui stabilisent et régulent les populations.
C'est ainsi, qu'actuellement aux États-Unis, les scientifiques considèrent que les Cervidés manquent de prédateurs. William Ripple et Robert Beschta (université de l'Oregon, États-Unis) ont réalisé en 2012 une compilation d'une quarantaine d'études réalisées au cours des 50 dernières années. Cette étude montre que, faute de grands prédateurs comme le Loup ou l'Ours, les populations de cerfs et de rennes ont atteint des niveaux record et menacent les écosystèmes dans les forêts boréales et tempérées de l'hémisphère Nord. Ainsi, dans les régions où le Loup est absent, les cervidés sont jusqu'à six fois plus nombreux. Les chercheurs notent qu'en contribuant à la déforestation, les cervidés ont un impact sur la capacité de la forêt de séquestrer du carbone et donc sur le changement climatique. Les scientifiques plaident donc pour la préservation ou la réintroduction des grands prédateurs, qui permettrait selon eux une régulation des populations d'herbivores et contribuerait ainsi au maintien de la biodiversité.
[1] L'isocline correspond aux différentes valeurs des effectifs de la proie et du prédateur pour lesquelles leurs populations respectives sont stables (dN / dt = 0).
[2] Cette loi donne une explication théorique des pullulations de ravageurs observées dans les cultures après réalisation de traitements pesticides. L'effet du toxique est indépendant de la densité et provoquera - toutes choses égales par ailleurs - une proportion égale de morts dans la population d'insectes ou autres arthropodes nuisibles et dans celles de leurs ennemis naturels : prédateurs et parasites. Il résultera de tout cela un nouvel état d'équilibre où le ravageur (proie) sera plus abondant et les auxiliaires moins nombreux, d'où la nécessité d'un nouveau traitement et ainsi de suite.
Sources :
- Barbault R. (1981) - Écologie des populations et des peuplements, 200 p. Masson Éd.
- Guyard A. (1997). - Cours de maîtrise. Option Peuplements et populations. Univ. Franche-Comté.
- Ramade F. (1987) - Éléments d'écologie. Écologie fondamentale, 403 p. McGraw-Hill Éd.
Plus de renseignements sur le Loup en France :
http://loup.org/spip/IMG/pdf/ddploupsfepm_dec2012.pdf
17:53 Publié dans Environnement-Écologie, Mammifères | Tags : prédation, populations, relations mangeur-mangé, modèles mathématiques de la prédation, lotka, volterra, croissance des populations, prédateur-proie | Lien permanent | Commentaires (8) | ![]() Facebook | | |
Facebook | | |


