L'échantillonnage
16/06/2010
L'ÉCHANTILLONNAGE
Dans un espace donné, il est rarement possible de dénombrer tous les individus composant une population biologique. D'où la nécessité d'effectuer un échantillonnage au sein de cet espace.
I. L'ÉLÉMENT D'ÉCHANTILLONNAGE
L'élément ou unité d'échantillonnage est une entité sur laquelle on observe la variable étudiée. L'élément est souvent lié à l'instrument de récolte ou d'observation.
Ex : pour dénombrer les populations de Melanoides tuberculata, mollusque compétiteur dans les cressonnières de Martinique de Biomphalaria glabrata, vecteur de la Bilharziose, on procède par carottage à l'aide de boîtes à base carrée (pots-pièges). L'élément correspond à la surface de la boîte et la variable au nombre de mollusques yi présents dans chaque boîte.
Ex : dans le cas de la pêche aux filets verticaux sur les lacs du Jura, l'unité d'échantillonnage est constituée par une batterie de 6 filets verticaux. La variable est le nombre de corégones capturés dans chaque batterie.
L'élément d'échantillonnage est une prise d'information sur le terrain qui peut requérir plusieurs formes :
1. Le relevé
est une prise directe sans prélèvement concret d'objets sur le terrain : relevé climatologique, topographique, phytosociologique sur des placettes ou quadrats, enregistrements sur analogiques…
2. Le prélèvement
retire les données du terrain (prélevat) pour l'analyse et suppose la destruction de la prise, produit du prélèvement.
Selon leurs caractéristiques spatiales, les prélevats peuvent être :
- euclidiens : cotés en unités de volume. Ils permettent des inférences (extrapolations ou interpolations) à un espace euclidien de dimensions supérieures au prélevat.
- Souvent, la composante verticale (hauteur) du champ écologique est négligée : on parle alors de prélevats cartésiens liés exclusivement à des cotes horizontales (surface) et de durée.
- Parfois les prélevats sont linéaires : l'information est alors acquise le long d'un transect, les autres dimensions euclidiennes étant ignorées.
- Ils peuvent être ponctuels, et dans ce cas organisés en séries dans le champ écologique et dans le temps selon un plan d'échantillonnage défini. Ils peuvent être informes (régime alimentaire d'un prédateur, individu-compartiment) ou cotés.
- L'association des prélevats en série peut être synchronique avec des caractéristiques de temps simultanées ou diachronique (mêmes lieux, dates différentes).
3. L'interception
est le mode d'obtention des données-cinèses par opposition aux données d'état. Une interception-relevé permet d'obtenir directement une donnée ou un analogique cinétique (anémomètre, rhéomètre, comptage d'oiseaux passant un col, lecture radar de papillons ou de poissons). Il y a traduction en débit effectif/temps (ex : nombre d'oiseaux par heure) parfois exprimé en tant que vitesse en considérant la section du passage : il s'agit alors de flux (vitesse/surface).
4. La prise
est un objet concret qui n'est plus dans le champ écologique mais qui fournira après analyse des données sur ce champ : prises de prélèvement, analogiques de relevés (photos), d'interception-relevé (bande d'un thermo-hygrographe) et les produits de l'interception-prélèvement (pot-piège).
II. ÉCHANTILLONS ET PLAN D'ÉCHANTILLONNAGE
L'ensemble des unités d'échantillonnage possibles dans le champ écologique étudié constitue la population statistique sur laquelle s'appliqueront les calculs relatifs au traitement des données.
On appelle échantillon, un groupe d'unités d'échantillonnage de même dimension tiré d'une population statistique préalablement définie, conformément à un plan de sondage et sur lesquelles porteront les observations prévues par l'enquête. Dans le cas d'un échantillonnage pour dénombrement, l'information de base est obtenue par dénombrement des individus de tous les éléments de l'échantillon. Le nombre d'individus par élément est la variable yi à étudier.
À la notion d'échantillon est étroitement associée la notion de plan d'échantillonnage. La planification de l'échantillonnage est une pratique courante dans les enquêtes sociologiques, économiques ou d'opinion. Les sondages effectués avant les élections s'appuient sur une planification très rigoureuse des protocoles d'enquête dont dépendra la présentation et le traitement des données.
La planification de l'échantillonnage apporte divers bénéfices :
- elle permet notamment de minimiser le coût de la collecte des données, ou, à coût fixe, d'optimiser la précision des résultats ;
- elle constitue un préalable indispensable au traitement statistique des données ;
- elle oblige à un effort de réflexion qui facilite l'organisation du travail sur le terrain.
Sous le terme de plan d'échantillonnage, on entend les divers protocoles mis en œuvre lors de la collecte des données sur le terrain en vue d'assurer l'objectivité des observations et l'économie des moyens.
La population statistique est une collection d'éléments :
- possédant au moins une caractéristique commune permettant de la définir ;
- de laquelle on extrait un échantillon représentatif ;
- sur laquelle porteront les calculs statistiques.
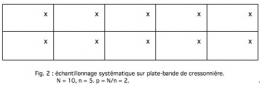
Dans le premier exemple, la population statistique N est la somme des surfaces de base du pot-piège contenue sur l'ensemble de la cressonnière (c'est-à-dire la surface de la plate-bande). L'échantillon n est le nombre de pots-pièges retenus (10 par plates-bandes de 50 m2). La variable yi est le nombre de mollusques par pot.
Dans le second exemple, la population statistique est le volume du lac.
La population-cible est la population à laquelle on pourra appliquer les conclusions de l'enquête.
Dans le premier exemple, la population-cible est la population de M. tuberculata présente dans la cressonnière au moment de l'intervention.
Dans le second cas, la population-cible sera la population de corégones présents dans le lac à la date d'intervention et accessible à la capture.
Dans le cas du saturnisme des canards par suite d'ingestion de grains de plomb,
- la population statistique est l'ensemble des canards colverts ayant avalé des plombs ;
- la population-cible est l'ensemble des colverts ;
- la population biologique est l'ensemble des colverts ou des anatidés fréquentant les lacs ou étangs étudiés.
En médecine, dans le cas du SIDA,
- la population statistique est l'ensemble des porteurs du virus HIV accessible au chercheur ;
- la population-cible est l'ensemble des personnes séro-positives.
En élevage, la population statistique se confond avec la population-cible et la population biologique (ex : rats, souris, lapins).
Le statisticien applique ses conclusions à la population statistique. La généralisation des résultats à la population-cible se fait aux risques et périls du biologiste.
III. QUELQUES TYPES DE PLANS D'ÉCHANTILLONNAGE
De nombreux types de plans d'échantillonnage ont été mis au point par de nombreux auteurs. On trouvera ci-dessous quelques plans d'échantillonnage universellement reconnus.
1. Échantillonnage aléatoire simple (EAS)
1.1. Définition
C'est une méthode qui consiste à prélever au hasard et de façon indépendante n unités d'échantillonnage d'une population statistique comportant N unités. Ainsi, chaque élément de la population statistique présente la même probabilité de faire partie d'un échantillon de n unités et chacun des échantillons possibles de taille n présente la même probabilité d'être constitué.
1.2. Protocole de sélection des unités d'échantillonnage
Pour que nulle erreur systématique ne s'introduise dans la constitution de l'échantillon, il faut dresser la liste complète et sans répétition des éléments de la population statistique, les numéroter de 1 à N puis procéder au tirage au sort de n unités différentes à l'aide d'un dispositif de génération de nombres aléatoires.
Ces opérations de prélèvements se révèlent assez faciles si la population statistique n'est pas trop grande et si les éléments sont facilement identifiables ou repérables. Elles sont assez commodes s'il s'agit de positionner dans l'espace ou dans le temps une station de prélèvement, un itinéraire-échantillon (transect) ou un quadrat puisque l'énumération des coordonnées géographiques ou temporelles ne nécessite pas un inventaire fastidieux des éléments. Toutefois, il est difficile de réaliser en écologie un échantillonnage aléatoire simple qui se conforme scrupuleusement à la définition.
1.3. Avantages du plan
• Le plan EAS est universellement reconnu et accepté.
• Aucune préinformation n'est requise pour sa mise en application, contrairement à la majorité des autres plans. La préparation du protocole n'exige en effet aucune pré-enquête et les différentes estimations sont calculées à partir des données recueillies sur l'échantillon sans faire appel à d'autres renseignements.
• Les estimateurs ne sont pas biaisés, leur calcul est facile, la majorité des programmes informatiques se prêtent à ce plan et les techniques statistiques multidimensionnelles sont applicables.
1.4. Inconvénients du plan
• L'inventaire des éléments de la population statistique est souvent une opération difficile et parfois impossible surtout si la population statistique correspond à une population biologique. Par exemple, l'échantillonnage des animaux et des plantes sauvages se heurte à l'abondance, la mobilité, la dispersion, le cryptisme des éléments qui ne peuvent être énumérés.
Ex : Ingestion de plombs de chasse ingérés par les Anatidés.
Les canards ingèrent des plombs de chasse avec les graviers qu'ils utilisent dans leur gésier et sont atteints de saturnisme.
Population statistique : nombre de colverts abattus.
Variable : nombre de plombs ingérés par canard.
Population-cible : population de colverts sur l'étang/ou de canards/ou de sauvagine.
Population biologique : anatidés/ou canards.
• Quand les unités d'échantillonnage sont constituées par des animaux, la sélectivité des moyens de capture ne permet pas un prélèvement au hasard et introduit un biais dans l'échantillonnage dont il faut apprécier l'importance et le sens (sur- ou sous-estimation). Par exemple, si des engins de capture sont répartis aléatoirement dans un espace donné, les spécimens récoltés ne sont pas pour autant prélevés selon les principes de l'EAS car la majorité des pièges s'avèrent sélectifs. Le plan peut éventuellement prétendre être correct pour la sélection des unités de la population statistique (ici les unités territoriales) mais pas pour la population animale-cible.
• L'efficacité du plan EAS est souvent médiocre car toute expérience antérieure ou concomittante est ignorée. On ne collecte pas préférentiellement des éléments privilégiés dont l'accès ou l'examen est plus commode ou plus économique. On ne module pas la probabilité de sélection des éléments en fonction de leur poids ou de leur importance relative. Ainsi le coût de l'échantillonnage n'est pas optimisé relativement à la précision des résultats.
2. Échantillonnage systématique (SYS)
1.1. Définition
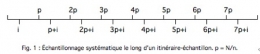
C'est une technique qui consiste à tirer au hasard un i-ième élément situé entre le premier et le p-ième de la population statistique, puis à prélever systématiquement le (i + p)-ième, le (i + 2p)-ième, le (i + 3p)-ième… élément de la population (fig. 1 et 2). On obtient finalement n unités collectées selon un classement fondé sur une progression arithmétique dont la base est un nombre aléatoire i et la raison un nombre p calculé de telle sorte que l'échantillon se répartisse uniformément sur toute la population statistique. Contrairement à l'EAS, les unités ne sont pas prélevées indépendamment les unes des autres puisque le choix de i et de p détermine la composition de tout l'échantillon.
1.2. Protocole de sélection des unités d'échantillonnage
Il est simple quand les éléments de la population statistique sont accessibles et en nombre connu. On choisit n en fonction de l'effort d'échantillonnage consenti ; on calcule la raison p = N/n et on tire au hasard l'élément i compris entre 1 et p ; on effectue ensuite un prélèvement toutes les p unités.
Lorsque N est inconnu et qu'il est difficile d'en estimer l'ordre de grandeur, p est fixé arbitrairement. Il n'est donc plus possible de choisir l'effectif n. C'est au cours du déroulement des opérations qu'on jugera si la raison p est trop grande ou trop petite.
1.3. Avantages du plan
• Il est plus commode à mettre en œuvre que l'EAS. Ainsi, la répartition d'un ensemble de relevés dans un intervalle de temps ou au sein d'une population statistique linéaire (lit d'une rivière, lisière d'une forêt, route d'un navire) est facile à réaliser avec SYS.
• Si l'on est assuré que tous les éléments de la population statistique se présentent dans un ordre aléatoire, alors ce plan est équivalent à l'EAS dont il cumule les avantages avec les siens propres.
• Si la population biologique présente des phénomènes d'autocorrélation positive, c'est-à-dire si les descriptions yi et yj sont d'autant plus semblables que les éléments i et j sont proches, SYS est plus efficace que EAS. En effet, par le fait du hasard, l'EAS comporte des relevés rapprochés qui apportent une information redondante et d'autres éloignés entre lesquels la variable étudiée est mal représentée. Les phénomènes d'autocorrélation ne sont pas rares en écologie. Par exemple, les variations dans l'espace et dans le temps des conditions météorologiques sont corrélées positivement. Mattern (1960) a montré que les stations d'échantillonnage corrélées positivement devaient être disposées spatialement en quinconce, disposition qui maximise la distance entre relevés.
• Si les éléments de la population statistique présentent une tendance linéaire au niveau de la variable étudiée, SYS est alors plus efficace que EAS. Un tel type de variations est fréquent en écologie : gradient d'altitude, de profondeur d'eau, de salinité, d'émersion, de hauteur de végétation, évolution temporelle d'un phénomène naturel : recrutement d'une population…
1.4. Contraintes et inconvénients du plan
• Si la population présente une structure périodique et que la période p de prélèvement est proche de la longueur d'onde des variations du phénomène à étudier ou d'un multiple entier de celle-ci (harmonique), alors une importante erreur systématique est créée.
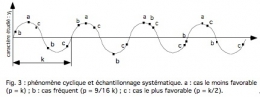
• Or en écologie, les phénomènes cycliques sont fréquents : rythmes saisonniers, lunaires, circadiens ; fluctuations d'abondance de certaines populations animales ou végétales (fig. 3). Par exemple, ce n'est pas avec des prises espacées de 24 heures qu'on mettra en évidence les migrations à rythme nycthéméral du plancton ou les émergences des furcocercaires des Schistosomes.
Dans le cas de plantations régulières ou dans le cas de rookeries (colonies d'individus regroupés), SYS peut générer un biais difficile à détecter lorsque les éléments de la périphérie diffèrent de ceux du centre.
• Comme l'EAS, SYS n'utilise pas des relevés antérieurs ou concomittants. Il ne permet pas de collecter préférentiellement des éléments privilégiés dont l'accès ou l'examen serait plus commodes. Enfin, il n'ajuste pas la probabilité de sélection des éléments en fonction de leur poids ou de leur importance relative.
3. Échantillonnage stratifié (STR)
1.1. Définition
L'échantillonnage stratifié (STR) est une technique qui consiste à subdiviser une population statistique hétérogène en sous-populations ou strates plus homogènes, mutuellement exclusives et collectivement exhaustives. La population statistique hétérogène d'effectif N est ainsi découpée en k strates plus homogènes d'effectif Nk tels que N = N1 + N2 + N3 + … + Nk. Un échantillon indépendant est ensuite prélevé au niveau de chaque strate en appliquant un plan d'échantillonnage au choix de l'opérateur.
1.2. Protocole de sélection des unités d'échantillonnage
L'application de ce plan soulève deux questions principales :
- comment construire les strates ?
- quels efforts et plans d'échantillonnage adopter dans chaque strate pour obtenir le plein bénéfice de la stratification ?
• Critères de stratification
Le choix du meilleur critère semblerait être la variable étudiée puisque le découpage de sa distribution de fréquence en différentes classes ou strates réduit automatiquement la variance intra-strates et augmente par le fait même, l'homogénéité au sein des strates. Ce critère n'est pas réaliste car il suppose la connaissance a priori du phénomène à étudier.
En pratique, on utilise une autre variable x, appelée stratificateur. Le stratificateur doit être corrélé le mieux possible avec la variable étudiée car plus la corrélation est étroite, plus le gain de précision apporté par la stratification est élevé.
Cependant le critère de stratification peut être qualitatif, ouvrant alors la porte à de multiples possibilités. Par exemple, dans un lac, on étudiera la répartition de telle espèce benthique en fonction de la profondeur ou de la nature du substrat : vase, sable, graviers, galets, blocs, litières, hydrophytes, bryophytes, algues, etc…, chaque substrat ou chaque profondeur constituant autant de strates plus homogènes que ne l'est l'ensemble du lac.
Le critère de stratification n'est pas forcément unique. Il peut y en avoir deux ou trois. On parle alors de double ou de triple stratification. Ex : profondeur et substrat, vitesse du courant et substrat…
• Nombre de strates
L'augmentation du nombre de strates améliore la précision mais accroît la lourdeur du protocole. Au delà de 5 à 6 strates, l'expérience montre que le gain de précision est généralement faible par rapport au surcroît de travail. Souvent le choix du nombre de strates est guidé par la nature de l'échantillonnage, notamment lorsque le critère est qualitatif : limites géographiques ou administratives, typologie de la végétation, nature des fonds d'un lac ou d'une rivière, etc… Même lorsque le critère est quantitatif, on peut préfixer le nombre de strates : 8 cases S-V dans l'IBGN ; structure d'âge d'une population déjà distribuée en classes de taille qui constituent autant de strates.
• Limites des strates
Si le critère de stratification est qualitatif, il faut et il suffit de définir clairement les frontières entre chaque strate de façon à éviter les ambiguïtés. Par exemple, vases, sables, graviers, galets, blocs seront définis par une échelle granulométrique.
Si le critère de stratification est quantitatif, les limites des strates peuvent être définies par des contraintes préalables (cf plus haut : classes d'âge et classes de taille).
Si le critère de stratification est quantitatif, sans contraintes préalables, on doit fixer des limites minimisant la variance des estimateurs.
• Effort d'échantillonnage dans chacune des strates
Il s'agit de déterminer l'effectif des échantillons dans chaque strate. Trois stratégies d'allocation peuvent être développées à cet égard.
- L'allocation proportionnelle consiste à prélever un échantillon dont l'effectif nh est directement proportionnel à l'effectif Nh de la strate h. Ce type d'allocation a l'avantage de conduire à un protocole d'échantillonnage simple à mettre en œuvre.
- L'allocation optimale consiste à moduler l'effort d'échantillonnage afin de minimiser le coût total de l'opération pour une précision données ou de maximiser la précision pour un coût total fixé. L'effectif nh de l'échantillon doit être d'autant plus élevé que la variance de la strate est grande, que son effectif Nh est élevé, que le coût unitaire d'échantillonnage ch est faible.
- L'allocation de compromis consiste à fixer un nombre minimal d'éléments dans chaque strate (règle du butoir), puis à effectuer intuitivement l'effort résiduel dans chaque strate en fonction des mêmes règles que précédemment, à savoir que nh sera d'autant plus élevé que Sh (richesse spécifique dans la strate h) et Nh seront grands et ch petit.
L'allocation optimale et, en principe, l'allocation de compromis supposent des informations prérequises sur chaque strate. Il est rare que l'on dispose a priori de telles informations. La règle est donc de procéder à une enquête préalable souvent sous la forme d'un double échantillonnage, ce qui malheureusement alourdit le protocole. Mais quand on s'adresse à une macrofaune ou à une macroflore, l'homogénéité d'une strate est souvent appréciée par l'observation directe, même si elle ne peut pas être rigoureusement planifiée. Dans ce cas, l'allocation proportionnelle, voire une allocation largement intuitive sont recevables.
• Choix du plan d'échantillonnage dans chaque strate
Dans la mesure où l'échantillonnage d'une strate est totalement indépendant de celui d'une autre, il n'est pas nécessaire de choisir le même plan d'échantillonnage dans chaque strate. N'importe quel plan est donc recevable sous réserve d'en tenir compte pour les traitements statistiques ultérieurs. Dans la majorité des cas, le choix d'un EAS qui consiste à prélever un échantillon aléatoire dans chacune des strates est le plus judicieux.
Mais on peut procéder à une stratification de 2e ordre dans tout ou partie des strates de 1er ordre. Par exemple, si dans une population de poissons, on étudie la relation taille-poids et que les caractères sexuels sont visibles sur les 2+ (animaux dans leur 3e année), il est recommandé de faire deux sous-strates, l'une des mâles, l'autre des femelles dans chacune des strates de 1er ordre où le sexe est reconnaissable.
1.3. Avantages du plan
• Même très rudimentaire, la stratification apporte des gains de précision appréciables. C'est la méthode adoptée dans l'IBGN, les pêches en lac, l'étude des sédiments lacustres.
• Ce plan permet de profiter de situations particulières, chaque situation s'identifiant à une strate. C'est le cas quand des divisions naturelles facilitent le découpage du domaine à échantillonner, lorsque plusieurs équipes se partagent le travail…
• Ce plan constitue une solution avantageuse au problème de l'optimisation de l'effort d'échantillonnage.
1.4. Inconvénients du plan
• STR nécessite une planification rigoureuse des protocoles et entraîne des calculs laborieux.
• Une erreur d'appréciation des strates (rapport Nh/N) entraîne un biais considérable.
• Un critère de stratification qualitatif doit être judicieusement choisi.
• Un critère quantitatif sans contraintes préalables nécessite souvent un double échantillonnage et, par conséquent, un grand nombre de prélèvements. Il faut donc choisir un critère de stratification simple.
• Ce plan restreint le champ d'application des techniques habituelles de statistiques multidimensionnelles.
4. Échantillonnage avec régression (REG)
1.1. Définition
C'est une méthode qui consiste à corriger l'estimation Ŷ de la moyenne d'un échantillon aléatoire en fonction des résultats obtenus sur une variable auxiliaire x. Cet ajustement, qui repose sur la corrélation existant entre les variables y et x et sur la connaissance ou l'obtention de la moyenne X de la population, s'exprime dans le second terme du modèle de régression linéaire suivant :
1.2. Exemples
• Étude portant sur les réserves lipidiques des oiseaux migrateurs
La capacité migratoire d'un oiseau est fonction des réserves lipidiques qu'il accumule. La détermination de la quantité totale de graisse d'un oiseau entraîne le sacrifice de l'animal et un ensemble d'opérations réclamant plusieurs heures par animal.
Une autre méthode plus approximative consiste à apprécier visuellement la quantité de graisse sous-cutanée déposée dans la fosse claviculaire. L'indice d'adiposité qui en résulte s'évalue en quelques secondes et l'oiseau examiné peut poursuivre sa migration. Le double échantillonnage en vue de l'estimation par régression est particulièrement bien indiqué dans ce cas, car l'indice d'adiposité, facilement mesurable sur un grand nombre n' d'oiseaux peut alors servir de variable auxiliaire x et la quantité yi de graisse, difficile à mesurer, peut être déterminée sur quelques-uns (n) des n' oiseaux capturés. Scherrer (1972) trouve une corrélation élevée (0,9) entre les deux variables sur une population de mésanges. Il montre que, dans ce cas et compte tenu du coût estimé des différentes opérations (durée et frais de déplacement), le gain de précision maximal est obtenu pour un rapport de n = 94 oiseaux sacrifiés pour n' = 1492 oiseaux examinés puis relâchés.
• Étude des sédiments lacustres du Jura
Il existe une corrélation de 0,95 entre la réflectance (ou albedo) du sédiment et sa teneur en carbonate de calcium et de -0,95 entre la réflectance et la teneur en matière organique. Bien que la régression ne soit pas linéaire, l'utilisation d'une abaque permet de remplacer de longues et coûteuses analyses chimiques par la simple mesure d'un paramètre physique qui sert de variable auxiliaire.
1.3. Avantages du plan
• REG s'impose quand la variable étudiée impose le sacrifice d'éléments qui doivent être préservées pour des raisons éthiques en raison de la rareté de l'espèce ou du rôle des individus dans la poursuite de l'expérience. Cette situation est courante en biométrie.
1.4. Inconvénients du plan
• REG ne s'emploie qu'avec des variables qualitatives simples. Il est inutilisable avec les pourcentages ou les variables quotients.
• La relation entre x (transformé ou non) et y doit être linéaire. Sinon, il faut stratifier et la contrainte relative à l'effectif devient importante (chaque nh ≥ 50).
• La majorité des programmes informatiques ne sont pas conçus pour ce plan.
5. Échantillonnage par degrés (DEG)
1.1. Définition
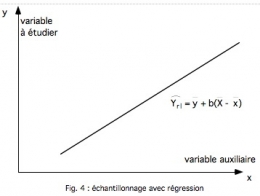
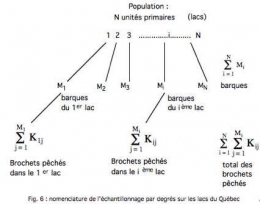
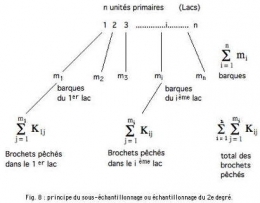
Cette méthode regroupe toute une batterie de plans d'échantillonnage caractérisés par un système ramifié et hiérarchisé d'unités (fig. 6-9).
Chacune des N unités de la population statistique appelées unités primaires ou grappes, se compose de Mi sous-unités plus petites appelées unités secondaires qui elles-mêmes peuvent comporter Kij unités tertiaires… À chaque niveau, un EAS peut être effectué. Si l'on en fait qu'un, on parle d'échantillonnage du 1er degré ; si l'on en fait deux, d'échantillonnage du 2e degré, si l'on en fait trois, d'échantillonnage du 3e degré…
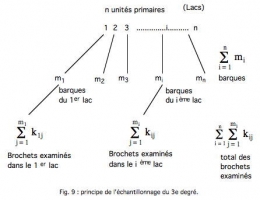
L'échantillonnage du 1er degré (échantillonnage par grappes) consiste à prélever aléatoirement n unités primaires ou grappes parmi les N unités primaires de la population et à mesurer les Mi sous-unités c'est-à-dire toutes les unités secondaires des n grappes sélectionnées.
L'échantillonnage du 3e voire du 4e degré constitue une extension de ce principe de sous-échantillonnage.
Les unités primaires, secondaires, etc… ne sont pas obligatoirement de la même taille. Si elles le sont, on pratique EAS et SYST.
1.2. Exemple
Pour étudier les caractéristiques des populations de poissons récoltés par des pêcheurs sportifs dans les parcs naturels du Québec, les biologistes du service de la faune utilisent l'échantillonnage du 3e degré. C'est de cette façon que la structure d'âge de la population de brochets est étudiée.
n lacs (unités primaires) sont choisis aléatoirement parmi les N lacs du parc ;
mi barques (unités secondaires) sont choisies parmi les Mi barques du i-ième lac échantillonné ;
kij brochets (unités tertiaires) des Kij brochets de la j-ième barque du i-ième lac sont prélevés aléatoirement en vue de l'extraction d'une écaille qui permettra la détermination de l'âge par scalimétrie.
1.3. Protocole de sélection des unités d'échantillonnage
• Définition des unités
Il s'agit de préciser quels sont les éléments, les grappes qui décomposent la population. En pratique,
- les grappes correspondent souvent aux structures de la population : pontes, nids, colonies, troupeaux ou bancs de poissons…
- les grappes peuvent être liées à la technique de récolte : prise d'un bateau, d'un filet, à plancton, d'une benne, d'un carottier…
- les grappes peuvent se rapporter à des entités naturelles composées d'éléments de dimensions arbitraires : bassin-versant ou lac.
Après avoir précisé la nature des différentes unités à tous les degrés de l'échantillonnage, il faut s'assurer que les grappes sont mutuellement exclusives et collectivement exhaustives. Ce qui revient à vérifier que le système d'unités qui se ramifie inclut toutes les unités élémentaires de la population et que chacune de ces dernières n'apparaît qu'une fois au sein des unités du niveau supérieur. L'exhaustivité est souvent difficile à apprécier en raison de la sélectivité des engins de capture. Ainsi, les filets à poissons ou à oiseaux, les pièges à insectes… constituent les grappes de la population capturée et non de l'ensemble de la population biologique puisque l'ensemble des pièges installés ne capture par la totalité de la population.
• Choix de la taille des éléments
Quand les éléments de la population sont naturels, la question ne se pose pas.
Il peut s'agir de quadrats, de périodes d'observation… dont on ne peut modifier la surface, le volume, la durée, c'est-à-dire la taille. Cette taille peut être déterminée par des méthodes normalisées.
En général, les plus petites unités sont les meilleures car elles autorisent la constitution de grands échantillons qui ont pour effet de diminuer le biais de certains estimateurs et d'accroître la robustesse de la majorité des tests. Ainsi, il sera préférable que le rapport de la surface ou du volume de l'entité examinée à la surface ou au volume de l'unité élémentaire d'échantillonnage soit inférieur ou égal à 0,05 (Green, 1979).
• Choix de la taille des grappes
Lorsque les grappes correspondent à des regroupements naturels, évidents ou obligatoires (lacs, barques), le problème du choix ne se pose pas.
Les grappes qui correspondent à des regroupements artificiels d'éléments sont construites soit intuitivement, soit à l'aide de méthodes d'optimisation. On tient compte des considérations suivantes :
- construire des grappes de même taille ;
- tenir compte des coûts engendrés par le passage d'une grappe à l'autre ou de l'exploration de grappes trop grandes ;
- choisir une unité fonctionnelle qui facilite le travail.
• Répartition de l'effort d'échantillonnage
Cette répartition se fait en tenant compte
- des coûts unitaires d'échantillonnage ;
- de la variabilité des données aux différents niveaux d'unités.
1.4. Avantages du plan
• DEG est peu contraignant car il ne requiert pas la liste complète ou un agencement particulier des éléments de la population statistique.
• Sur le terrain, DEG se révèle économique, facilement adaptable aux conditions particulières de chaque étude et peu perturbant sur l'ensemble étudié.
• DEG se combine facilement avec STR avec lequel il présente des convergences méthodologiques.
1.5. Inconvénients du plan
• DEG est moins efficace que EAS et SYS lorsque le coefficient de corrélation intra-grappe se révèle très élevé, c'est-à-dire quand les grappes se composent d'éléments qui se ressemblent beaucoup.
• Le calcul des estimateurs, l'application de certains tests d'hypothèses et de différentes techniques d'analyse multidimensionnelle est difficile.
• DEG nécessite une planification très élaborée. L'harmonisation de l'ensemble des opérations pour arriver à un protocole d'échantillonnage commode est complexe et longue.
V. CONCLUSION
Les quelques plans d'échantillonnage exposés ici ne sont pas exhaustifs. Il est possible de concevoir d'autres plans ou d'autres combinaisons de plans d'échantillonnage[1]. L'échantillonnage est une opération décisive et délicate qui demande certaines précautions.
Le traitement statistique des données (calcul des estimateurs, analyse des données) devra être effectué sur des exemples.
La réflexion sur l'échantillonnage doit toujours précéder la récolte des données. Planifier un échantillonnage, c'est répondre à trois questions :
- la manière d'observer est-elle pertinente pour ce que je veux observer ;
- les coûts consentis pour l'échantillonnage sont-ils répartis de manière à optimiser les observations ?
- les données recueillies sont-elles susceptibles d'être traitées par telle analyse statistique qui en facilitera l'interprétation ?
C'est en fonction des réponses à ces trois questions que chaque opérateur élaborera pour chaque étude son plan d'échantillonnage.
Source : Cours d'écologie de André Guyard
[1] Voir Scherrer B. dans Frontier S. (1983). - Stratégies d'échantillonnage en écologie. Masson Ed.

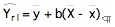
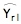
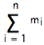
Les commentaires sont fermés.